Alhambra de Granada. Arabescos y geometría.

geometría en taqa, Sala de Dos Hermanas

Los progresos de traducción al árabe de textos filosóficos y científicos de la antigüedad fueron especialmente notables en el campo de las matemáticas y, más en concreto, en el de la geometría, donde, partiendo de los trabajos de grandes pensadores de la Grecia clásica como Euclides o Pitágoras, los eruditos musulmanes definieron un nuevo horizonte de posibilidades que, a nivel artístico, tuvo su plasmación en composiciones de una complejidad sin precedentes, vinculadas simbólicamente al ideal de perfección divina.

El arabesco tiene una finalidad artística distinta a la del arte figurativo y no trata de transportar a un mundo imaginado sino que, precisamente, libera de las ataduras de la imaginación. La repetición de un motivo fundamental de forma precisa, ordenada y matemáticamente perfecta induce a la contemplación. Motivos ornamentales de carácter geométrico cubren superficies de diferente amplitud en mosaicos, celosías, jambas y frisos de palacios y monumentos de la Alhambra en la ciudad de Granada.

En muchos de estos diseños cada parte del espacio posee una misma importancia. Se distingue una unidad de composición que, mediante una repetición sistemática, ocupa la superficie deseada. El estudio de este tipo peculiar de decoración nos sirve para introducirnos en el mundo de la geometría y realmente los arabescos de los palacios nazaríes de la Alhambra presentan una impresionante belleza geométrica.

medición de distancias sobre mosaico de Sala de los Reyes

Empecemos por el principio. Llamamos plano a una superficie prolongada indefinidamente. Los geómetras estudian en el plano figuras como circunferencias, triángulos, polígonos y otras formas geométricas. Uno de los problemas que se presenta más importante es distinguir si dos figuras son iguales y para ello se miden distancias y ángulos. 

En ocasiones no es sencillo medir una figura sin tener que moverla y es importante que, al moverla, no la deformemos, es decir, que el movimiento conserve las distancias y los ángulos. Así, en geometría euclídea, un movimiento es una transformación en el plano que a cada punto les hace corresponder, por una parte precisa, otro punto de modo que si dos puntos están a distancia R, sus transformados por el movimiento están de nuevo a esa misma distancia. Los movimientos en el plano son cuatro.

Reflexión. También llamado Simetría. Se toma una línea recta E en el plano, que se denominará Eje de reflexión, cada punto P tiene por imagen un punto P1 de modo que la recta que pasa por P y P1 es perpendicular al Eje de reflexión por lo que éste corta al segmento P - P1 por su punto medio. Esta transformación se origina tomando sobre el Eje de rotación un reflejo perpendicular al plano y se logra observar de forma extraordinaria en el Patio de los Arrayanes del Palacio de Comares, así como en el jardín del Palacio del Partal, con sus reflejos en el agua, elemento omnipresente en Alhambra, como Eje de reflexión o línea recta E.

movimiento de reflexión en el Patio de los Arrayanes

Rotación. También llamado Giro. Para el movimiento que conocemos como rotación existe un punto fijo en el plano y el resto de los puntos rotan en un ángulo prefijado. El punto fijo se denomina Centro de la rotación y el ángulo respectivo se conoce como Ángulo de rotación.

Traslación. El movimiento de traslación viene determinado por una flecha orientada que se denomina Vector de la traslación y cualquier punto P se transforma en otro punto P1. Una simetría de una figura en traslación ocupa un movimiento que la deja invariante.

Reflexión sesgada. También llamada Simetría con desplazamiento. Se trata de un movimiento de reflexión seguido de una traslación cuyo vector es paralelo al Eje de reflexión. La reflexión sesgada es una simetría del arabesco por desplazamiento.

Por su parte, un movimiento muy especial es aquel que, a cada punto P del plano, le hace corresponder el mismo punto P. Se trata del movimiento que deja todo como estaba y que se denomina movimiento identidad. Toda figura tiene por simetría el movimiento identidad. La realización de un movimiento seguido de otro es, a la vez, un movimiento más y a este nuevo movimiento se le denominará producto de los dos primeros.

simetrías en movimiento con Eje de reflexión en verde

Se abre así una operación algebraica para movimientos, definiendo que el producto de dos simetrías del arabesco que son traslaciones es otra traslación que también es simetría del arabesco. El producto de dos reflexiones cuyos ejes se cortan es una rotación y de nuevo el producto de dos simetrías es otra simetría pues se trata de un hecho general. El producto del movimiento identidad por otro movimiento es de nuevo tal movimiento. 

Por otra parte, para cada movimiento del plano existe otro por lo que el producto de ambos es el movimiento identidad y si se trata del movimiento que deshace al primero se denomina movimiento inverso. Si una figura o arabesco posee una simetría, el movimiento inverso de tal simetría es de nuevo una simetría del arabesco o de la figura, definiendo así otra operación; el producto sobre el conjunto de todos los movimientos.

Por tanto, se verifican las propiedades: (A x B) x C = A x (B x C), existiendo elemento identidad. 1 x A = A x 1 = A, existiendo elemento inverso y A x A-¹ = A-¹ x A = 1, teniendo así una estructura algebraica sobre el conjunto de todos los movimientos y también de las simetrías de una figura. Tal estructura algebraica se denomina grupo. 

propiedades de los grupos cristalográficos planos

Los grupos aparecen muy frecuentemente en matemáticas pues son la estructura que permite definir una igualdad o equivalencia y en nuestro caso define la igualdad de figuras planas, diciendo que dos figuras son iguales si existe un movimiento que transforma una en otra. Además de los movimientos existen otras transformaciones del plano como las homotecias o las transformaciones afines. 

Con estas nuevas transformaciones se pueden obtener grupos más amplios que el grupo de movimientos. Con tales grupos se define una noción nueva de igualdad de figuras lo que da lugar a otro tipo de geometrías. Si pensamos un arabesco que se extiende indefinidamente en el plano, tal arabesco puede tener simetrías que son traslaciones. Si un arabesco tiene un grupo de simetrías que contiene a dos traslaciones cuyos vectores no son paralelos entonces tal grupo de simetrías es un grupo cristalográfico plano.

Así, los grupos de simetrías de los arabescos dan lugar a los grupos cristalográficos planos, clasificándose debido a los tipos de movimientos que poseen. De los 17 grupos cristalográficos planos que existen, todos ellos cuentan -como ya sabemos- con al menos un ejemplo en el interior de los palacios nazaríes de Alhambra como grupos de simetrías de arabesco.

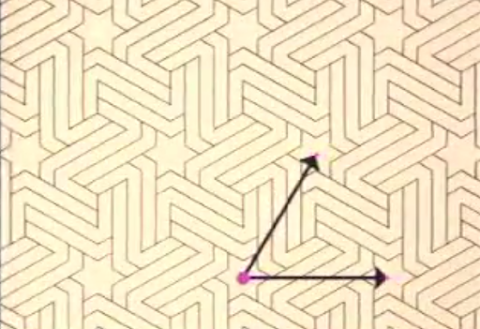simetría de traslación y 60º en yeserías de Sala de los Reyes

Tomemos un sólo ejemplo de grupo de simetrías. Aparece entre las múltiples yeserías de la Sala de los Reyes, en el interior del Palacio de Los Leones. Estas yeserías poseen simetrías que son traslaciones y los vectores de las traslaciones posibles son los representados sobre el diseño lanzando flechas. También poseen simetrías que son rotaciones de 60º, 120º y 180º y los nuevos centros de rotación de 60º, 180º y 120º vuelven a ser simetrías del arabesco. Este ejemplo de mosaico con su respectivo grupo de simetría, sin embargo, no posee simetrías que sean reflexiones. 

En estas yeserías de la Sala de los Reyes, el grupo de simetrías del arabesco se denomina, siguiendo la anotación internacional de cristalografía, grupo cristalográfico p6. En las diversas estancias, zócalos en mosaico y monumentos de Alhambra, formando un poema matemático, podemos encontrar otros ejemplos de otros grupos como el grupo p4gm, p1, p1m, pmm, p3m1 o p4 por citar tan solo varios de ellos.